Cosine and sine are trigonometric functions. Cosine gives the ratio of the adjacent side to the hypotenuse, while sine gives the ratio of the opposite side to the hypotenuse.
The cosine and sine functions, represented as cos(θ) and sin(θ), respectively, are fundamental trigonometric functions that reveal the shape of a right triangle. These functions play a crucial role in trigonometry, describing the relationship between angles and sides in a triangle.
The cosine function represents the ratio of the adjacent side to the hypotenuse, while the sine function represents the ratio of the opposite side to the hypotenuse. They are used in various applications of trigonometry, such as calculating distances, angles, and harmonic oscillations.
Key Takeaways:
- The cosine and sine functions are essential trigonometric functions used to describe the relationship between angles and sides in a right triangle.
- Cosine represents the ratio of the adjacent side to the hypotenuse, while sine represents the ratio of the opposite side to the hypotenuse.
- They are used in various applications, from calculating distances and angles to analyzing harmonic oscillations.
- Understanding the key differences between cosine and sine is crucial for mastering trigonometry and its applications.
Visual Representation of Sine and Cosine

When it comes to understanding sine and cosine, visual representation can greatly enhance our comprehension. One effective way to visualize these trigonometric functions is through a right triangle. By examining the relationship between the sides of the triangle and the angles within, we can gain valuable insights into the behavior of sine and cosine.
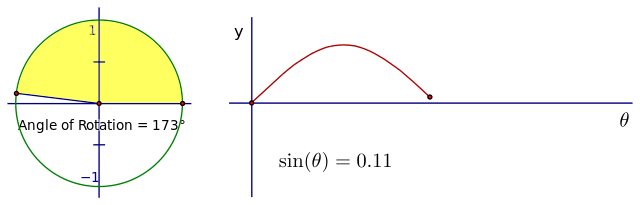
In particular, the unit circle provides a useful tool for visualizing sine and cosine. In this circle, the length of the hypotenuse of the right triangle is 1. This convenient choice of unit length allows us to easily determine the values of cosine and sine for various angles (θ).
By recording the values of x and y in the right triangle for different angles, we can find the values of sin(θ) and cos(θ). These values demonstrate the relationship between the angles and the lengths of the sides in the triangle.
Furthermore, the unit circle representation allows for the conversion between Cartesian coordinates (x, y) and polar coordinates (r, θ). This conversion enables us to relate the geometric properties of the right triangle to the algebraic coordinates on the plane.
Let’s take a look at a visual representation of sine and cosine using the unit circle:
This image showcases the unit circle and the corresponding values of sine and cosine for various angles. The visual representation helps us understand the periodic nature of these functions and how they vary with different angles in the unit circle.
In addition to visual representation, sine and cosine can also be approximated using mathematical series, such as the Taylor series. These series provide a way to express these trigonometric functions as infinite sequences of terms, allowing us to compute their values with increasing accuracy.
Summary:
- Visual representation, such as a right triangle and the unit circle, helps us grasp the behavior of sine and cosine.
- The unit circle representation conveniently uses a hypotenuse length of 1 to determine the values of sine and cosine for different angles.
- The unit circle facilitates the conversion between Cartesian coordinates and polar coordinates.
- This visual representation enhances our understanding of the periodic nature and variation of sine and cosine.
Relationship Between the Graphs of Sine and Cosine
The graphs of the sine function (y = sin x) and the cosine function (y = cos x) exhibit a unique relationship in trigonometry. The cosine graph is essentially a shifted version of the sine graph by 90 degrees or π/2. Let’s explore this relationship and understand how it is represented graphically.
Cofunction Identities
The relationship between the graphs of sine and cosine can be explained using cofunction identities. These identities define the function values of complementary angles in a right triangle. One of the most well-known cofunction identities states that cosθ = sin(90° – θ). This means that the cosine value of an angle is equal to the sine value of its complement or the angle obtained by subtracting the original angle from 90 degrees.
By applying this cofunction identity, we can determine that the graphs of sine and cosine only differ by a shift of 90 degrees or π/2. Let’s take a closer look at how this translates into graphical representations.
Graphical Representation
The graphs of sine and cosine can be plotted on a coordinate plane, with the x-axis representing the angle and the y-axis representing the function value. The graph of the sine function, denoted as y = sin x, has a characteristic wave-like shape. On the other hand, the graph of the cosine function, represented as y = cos x, exhibits a similar shape but is shifted horizontally by 90 degrees or π/2.
To better visualize this relationship, let’s take a look at the graphs of sine and cosine:
| Angle (x) | Sine Function (y = sin x) | Cosine Function (y = cos x) |
|---|---|---|
| 0° | 0 | 1 |
| 90° | 1 | 0 |
| 180° | 0 | -1 |
| 270° | -1 | 0 |
| 360° | 0 | 1 |
As observed from the table and the graph, the sine function oscillates between the values of 1 and -1, while the cosine function oscillates between the values of 1 and -1, but starting from a different point. The relationship between the graphs is clearly visible, with the cosine graph being a shifted version of the sine graph.
This relationship between the graphs of sine and cosine is crucial in trigonometry and finds application in various mathematical and physical concepts. Understanding this relationship helps in solving trigonometric equations, analyzing waveforms, and modeling periodic phenomena.
Extension of Sine and Cosine to Real Numbers
Sine and cosine are not limited to right triangles; they can be extended to any real value using the polar coordinate system. This system allows us to represent any (x, y) point as an alternative (r, θ) point. Here, r represents the distance from the origin to the point, and θ represents the angle between the segment connecting the origin and the point and the positive x-axis.
The conversion rule from Cartesian to polar coordinates is (x, y) = (rcos(θ), rsin(θ)). This extension of sine and cosine to the polar coordinate system provides a deeper understanding of the relationship between angles, coordinates, and trigonometric functions.
One way to visualize the extension of sine and cosine to real numbers is through the use of a unit circle. The unit circle represents a circle with a radius of 1, centered at the origin. By considering different angles (θ), we can find the corresponding values of sin(θ) and cos(θ). These values can be approximated using mathematical series, such as the Taylor series. The unit circle representation also allows for easy conversion between Cartesian coordinates (x, y) and polar coordinates (r, θ).
Let’s take a look at an example to illustrate the extension of sine and cosine to real numbers using the polar coordinate system:
| Cartesian Coordinates (x, y) | Polar Coordinates (r, θ) |
|---|---|
| (1, 0) | (1, 0) |
| (0, 1) | (1, π/2) |
| (-1, 0) | (1, π) |
| (0, -1) | (1, 3π/2) |
| (1, 1) | (√2, π/4) |
By representing points in both Cartesian and polar coordinates, we can see how the extension of sine and cosine to real numbers provides a different perspective on trigonometric functions and their relationship to angles and coordinates.
Additional Representations of Sine and Cosine
Aside from their geometrical interpretations and polar coordinate representations, sine and cosine can also be defined using complex numbers and differential equations. These alternative representations provide alternate ways to derive the properties and identities of sine and cosine.
Complex Numbers
Complex numbers offer a powerful way to define sine and cosine functions in the entire domain of complex numbers. By utilizing the exponential function and Euler’s formula, sine and cosine can be expressed in terms of complex numbers. This allows for a deeper understanding and analysis of their behavior in both real and imaginary domains.
Differential Equations
Differential equations provide another avenue for representing the behavior of sine and cosine. By modeling the relationship between the rate of change of a function and the function itself, differential equations allow for a more comprehensive understanding of the properties and dynamics of sine and cosine.
Taylor Series and Continued Fractions
Sine and cosine functions can also be represented as infinite series. The Taylor series is a mathematical tool that approximates functions using an infinite sum of terms. By expanding the sine and cosine functions into their respective Taylor series, we can gain insight into their behavior and use them for various calculations. Additionally, continued fractions provide a unique way to express sine and cosine as an infinite sequence of terms, enabling a different perspective on their properties.
| Representation Method | Description |
|---|---|
| Complex Numbers | Define sine and cosine in the complex plane using Euler’s formula and the exponential function. |
| Differential Equations | Model the behavior of sine and cosine using differential equations that relate their rate of change to the functions themselves. |
| Taylor Series | Approximate sine and cosine by expanding them into infinite series, providing a powerful tool for calculations and analysis. |
| Continued Fractions | Represent sine and cosine as an infinite sequence of terms, offering an alternate perspective on their properties. |
Reciprocals and Inverses of Sine and Cosine
The reciprocal functions of sine and cosine play an important role in trigonometry. The reciprocal of sine is known as cosecant (csc), while the reciprocal of cosine is called secant (sec).
Reciprocal Functions
The cosecant function (csc) is defined as the ratio of the hypotenuse to the opposite side in a right triangle. It can be calculated using the equation csc(θ) = 1/sin(θ), where θ represents the angle.
Similarly, the secant function (sec) is the ratio of the hypotenuse to the adjacent side. It can be expressed as sec(θ) = 1/cos(θ).
Inverse Functions
Inverse functions allow us to find the angle whose sine or cosine value is a given number. The inverse of sine is called arcsine (or inverse sine), denoted as arcsin(x) or sin^(-1)(x). It returns the angle θ such that sin(θ) = x. For example, arcsin(0.5) gives the angle whose sine is 0.5.
The inverse of cosine is known as arccosine (or inverse cosine) and is represented by arccos(x) or cos^(-1)(x). It gives the angle θ such that cos(θ) = x. For instance, arccos(0.5) provides the angle whose cosine is 0.5.
Trigonometric Identities and Pythagorean Identity
Trigonometric identities are mathematical equations that define relationships between trigonometric functions. These identities play a crucial role in simplifying expressions involving sine and cosine and proving various mathematical results.
One of the most well-known identities is the Pythagorean identity, which states that sin^2(x) + cos^2(x) = 1. This identity holds true for all values of x and is derived from the properties of right triangles. It demonstrates the fundamental relationship between the sine and cosine functions.
The Pythagorean identity is significant in trigonometry as it relates the square of sine and cosine to the value 1. This relationship can be observed in various contexts, such as when examining right triangles or analyzing the behavior of waves.
Trigonometric identities enable the simplification of complex trigonometric expressions by utilizing the fundamental properties and relationships of sine and cosine. These identities are widely used in calculus, physics, engineering, and other scientific disciplines.
Here are some commonly used trigonometric identities:
- Sum and Difference Identities: These identities express the sine and cosine of the sum or difference of two angles in terms of the sines and cosines of the individual angles.
- Double-Angle Identities: These identities relate the sine and cosine of double an angle to the sines and cosines of the original angle.
- Half-Angle Identities: These identities express the sine and cosine of half an angle in terms of the sines and cosines of the original angle.
| Identity | Description |
|---|---|
| Sine Addition | sin(A + B) = sin(A)cos(B) + cos(A)sin(B) |
| Cosine Addition | cos(A + B) = cos(A)cos(B) – sin(A)sin(B) |
| Sine Subtraction | sin(A – B) = sin(A)cos(B) – cos(A)sin(B) |
| Cosine Subtraction | cos(A – B) = cos(A)cos(B) + sin(A)sin(B) |
| Sine Double-Angle | sin(2A) = 2sin(A)cos(A) |
| Cosine Double-Angle | cos(2A) = cos^2(A) – sin^2(A) |
| Sine Half-Angle | sin(A/2) = ±√((1 – cos(A))/2) |
| Cosine Half-Angle | cos(A/2) = ±√((1 + cos(A))/2) |
Trigonometric identities provide powerful tools for solving mathematical problems and analyzing various phenomena in nature and science. The Pythagorean identity serves as a key foundation for understanding the interplay between sine and cosine and their applications in different fields.
Derivatives and Integrals of Sine and Cosine
In calculus, the derivatives and integrals of sine and cosine are fundamental concepts that extend the understanding and application of these trigonometric functions. Understanding their derivatives and integrals is essential in various fields of mathematics, physics, and engineering.
The derivative of the sine function, sin(x), with respect to x is the cosine function, cos(x). It represents the rate of change of the sine function with respect to x. Similarly, the derivative of the cosine function, cos(x), with respect to x is the negative sine function, -sin(x). It represents the rate of change of the cosine function with respect to x.
The antiderivative (or integral) of the sine function, sin(x), is -cos(x), and the antiderivative of the cosine function, cos(x), is sin(x). The antiderivative represents the reverse process of finding the original function given its rate of change.
These derivatives and integrals are integral in calculus, as they allow us to solve various problems involving trigonometric functions. For example, in physics, the derivatives and integrals of sine and cosine are used to model periodic phenomena, such as harmonic oscillations.
Derivatives and Integrals of Sine and Cosine Summary
To summarize, the derivatives of sine and cosine with respect to x are as follows:
| Trigonometric Function | Derivative |
|---|---|
| Sine (sin(x)) | Cosine (cos(x)) |
| Cosine (cos(x)) | Negative Sine (-sin(x)) |
Similarly, the integrals (antiderivatives) of sine and cosine are as follows:
| Trigonometric Function | Integral (Antiderivative) |
|---|---|
| Sine (sin(x)) | -Cosine (-cos(x)) |
| Cosine (cos(x)) | Sine (sin(x)) |
These derivatives and integrals serve as powerful tools in calculus, enabling us to solve complex problems and analyze the behavior of functions involving sine and cosine.
Applications and Uses of Sine and Cosine
Sine and cosine functions play a crucial role in modeling and analyzing various periodic phenomena. These fundamental trigonometric functions provide valuable insights into the behavior of sound waves, light waves, harmonic oscillators, position, velocity, temperature variations, and more.
Sound Waves and Light Waves
Examining the properties of sound waves and light waves is essential in fields such as acoustics and optics. Sine and cosine functions help describe the periodic nature of these waves, including their amplitudes, frequencies, and phases. By analyzing the behavior of sine and cosine functions, scientists and engineers can better understand the propagation, interference, and diffraction of sound and light waves.
Harmonic Oscillators
Harmonic oscillators are systems that exhibit repeated motion, characterized by a restoring force proportional to displacement. Examples include the motion of a pendulum, swinging of a spring, or the vibrations of musical instruments. Sine and cosine functions provide a concise mathematical representation of the periodic motion observed in harmonic oscillators. They are key to analyzing the displacement, velocity, and acceleration of these systems over time.
Position, Velocity, and Distance
Sine and cosine functions are invaluable in determining the position, velocity, and distance of objects undergoing periodic motion. These functions can accurately describe the position and velocity of an object at any given time. Additionally, by integrating cosine or sine functions, the total distance traveled by an object can be calculated. This is particularly useful in physics, engineering, and navigation applications.
Temperature Variations and Climate Studies
Temperature variations are an example of a periodic phenomenon that can be analyzed using sine and cosine functions. By fitting temperature data to these functions, scientists can extract valuable information about seasonal changes, climate patterns, and long-term trends. This analysis can assist in studying the effects of climate change, predicting agricultural productivity, and informing energy usage optimization strategies.
Examples and Further Applications
The applications of sine and cosine functions extend far beyond the examples mentioned above. Here are a few more areas where these functions find widespread use:
- Robotics and motion control systems
- Electrical engineering and signal processing
- Seismic data analysis and earthquake monitoring
- Wireless communication and signal modulation
- Music theory and digital sound synthesis
- Financial market analysis and forecasting
| Application | Description |
|---|---|
| Robotics and Motion Control Systems | Sine and cosine functions are used to control robotic arm movements, drones, and other automated systems. They facilitate precise positioning, smooth transitions, and path planning, ensuring efficient and accurate operations. |
| Electrical Engineering and Signal Processing | Sine and cosine functions play a vital role in analyzing and manipulating electrical signals. They are used in applications such as audio processing, image and video compression, and digital signal filtering. |
| Seismic Data Analysis and Earthquake Monitoring | Sine and cosine functions are used to analyze seismic data and monitor ground vibrations. They help scientists interpret earthquake patterns, measure earthquake magnitude and frequency, and assess potential risks. |
| Wireless Communication and Signal Modulation | Sine and cosine functions are utilized in wireless communication systems for signal modulation, demodulation, and frequency shifting. They enable the transmission and reception of information through various wireless technologies. |
| Music Theory and Digital Sound Synthesis | Sine and cosine functions are central to music theory, allowing the generation of different musical pitches and tones through digital sound synthesis. By combining sine waves of varying frequencies, complex sounds can be produced. |
| Financial Market Analysis and Forecasting | Sine and cosine functions are employed in financial market analysis to identify cyclic patterns, detect market trends, and forecast future price movements. They are utilized in technical analysis methods such as moving averages and oscillator indicators. |
The wide range of applications and uses of sine and cosine functions highlights their relevance across various scientific, engineering, and mathematical disciplines. By understanding and harnessing the power of these functions, researchers and professionals can gain valuable insights into the behavior and characteristics of periodic phenomena.
Additional Considerations and History of Sine and Cosine
Sine and cosine functions have a rich history dating back centuries, with roots in ancient Indian astronomy during the Gupta period. This period saw the development and utilization of various trigonometric functions, including the jyā and koṭi-jyā functions, which laid the foundation for the study of sine and cosine.
One of the significant advancements in understanding sine and cosine came with the introduction of the unit circle representation. The unit circle, with a radius of 1, provides a convenient way to understand the properties and values of sine and cosine for different angles. This visual representation has become a standard method in the study of trigonometric functions.
Moreover, sine and cosine have been extended beyond their geometric interpretations, finding applications in complex numbers and differential equations. Complex numbers allow for the definition of sine and cosine in the entire domain of complex numbers, enhancing their mathematical significance. The study of differential equations further deepens the understanding of these functions and their role in various fields of mathematics and science.
To better visualize and understand these concepts, refer to the unit circle representation below:
Unit Circle Representation of Sine and Cosine
| Angle (θ) | Sine (sin θ) | Cosine (cos θ) |
|---|---|---|
| 0 | 0 | 1 |
| π/6 | 1/2 | √3/2 |
| π/4 | √2/2 | √2/2 |
| π/3 | √3/2 | 1/2 |
| π/2 | 1 | 0 |
The table above showcases the values of sine and cosine for some common angles within the unit circle. It demonstrates the relationship between angles and the corresponding sine and cosine values, providing a visual and numerical understanding of these fundamental trigonometric functions.
Conclusion
In conclusion, the cosine and sine functions play a vital role in trigonometry, offering valuable insights into the relationship between angles and sides in a right triangle. While cosine represents the ratio of the adjacent side to the hypotenuse, sine represents the ratio of the opposite side to the hypotenuse. These functions have multiple representations, including visual, geometric, polar coordinate, and complex number representations, which enable diverse applications in mathematics, science, and engineering.
The key differences between cosine and sine lie in the sides of the triangle they relate to. Understanding these differences is crucial for mastering trigonometry and leveraging its applications. By exploring the properties and identities of these functions, we can model and analyze various natural phenomena, such as sound waves, light waves, and harmonic oscillations.
In summary, the study of cosine and sine opens up a world of mathematical possibilities. From their origins in ancient Indian astronomy to their modern use in calculus and complex analysis, these functions continue to shape our understanding of the world around us. By grasping their fundamental principles and applications, we can unlock new insights and achieve greater proficiency in the field of trigonometry.
FAQ
What is the difference between cosine and sine?
The cosine function represents the ratio of the adjacent side to the hypotenuse in a right triangle, while the sine function represents the ratio of the opposite side to the hypotenuse.
How are sine and cosine visually represented?
Sine and cosine can be visually represented using a right triangle and the unit circle, where the values of x and y for different angles (θ) are recorded to find sin(θ) and cos(θ).
What is the relationship between the graphs of sine and cosine?
The graph of the cosine function is a shifted version of the sine graph by 90 degrees or π/2. The graphs differ only by this shift and are related through the cofunction identities.
How are sine and cosine extended beyond right triangles?
Sine and cosine can be extended to any real value using the polar coordinate system, allowing for the representation of (x, y) points as (r, θ) points.
Can sine and cosine be represented using other mathematical tools?
Yes, sine and cosine can be represented using complex numbers, differential equations, Taylor series, and continued fractions, providing alternative ways to derive their properties and identities.
What are the reciprocal functions and inverses of sine and cosine?
The reciprocal function of sine is cosecant (csc), and the reciprocal function of cosine is secant (sec). The inverses of sine and cosine are arcsine and arccosine.
Are there any useful trigonometric identities related to sine and cosine?
Yes, the Pythagorean identity sin^2(x) + cos^2(x) = 1 is one of the most well-known identities, derived from the properties of right triangles.
What are the derivatives and integrals of sine and cosine?
The derivative of sine is cos(x), and the derivative of cosine is -sin(x). The antiderivative of sine is -cos(x), and the antiderivative of cosine is sin(x).
What are the applications and uses of sine and cosine?
Sine and cosine functions are used to model and analyze periodic phenomena, describe harmonic oscillators, measure angles and distances, and study various cyclic phenomena in science and engineering.
Are there any historical considerations regarding sine and cosine?
Sine and cosine functions have a long history and can be traced back to ancient Indian astronomy during the Gupta period. The unit circle representation has become a standard approach for understanding their properties.
Source Links
- https://setosa.io/ev/sine-and-cosine/
- https://www.dummies.com/article/academics-the-arts/math/trigonometry/comparing-cosine-and-sine-functions-in-a-graph-186910/
- https://en.wikipedia.org/wiki/Sine_and_cosine
Image Credits
Featured Image By – Freepik
Image 1 By – macrovector on Freepik
Image 2 By – Adrignola, CC0, via Wikimedia Commons









